时空旅行(14-4)
该比赛已结束,您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。
题目背景
于道各努力,千里自同风。── 唐·杜甫《奉赠韦左丞丈二十二韵》
在毕业典礼上,Diana 回想起了许多精彩的往事,这些回忆仿佛发生在一系列事件节点之间,通过时空隧道相连。她希望再次“穿梭”回去,重温那些对她特别重要的瞬间。
题目描述
在 Diana 的回忆中,共有 个事件节点,分别为 。这些节点之间通过 条双向的时空隧道相连,隧道与节点都可以被多次穿越。
- 每条时空隧道有一个通行费用 ;
- 每个事件节点有一个“伤心值” ;
- 有 个节点对 Diana 尤其重要,它们组成关键事件集合 。
Diana 想从起始节点 出发,到达除 以外的每个目标节点 ,并且在到达 的路径上必须途经集合 中的所有节点(可按任意顺序、多次经过)。
请你计算,对于每个目标节点 ,满足上述条件的路径所需代价之和的最小值。代价包括:
- 路径上所有事件节点的伤心值之和(重复经过同一节点需重复累加,起点和终点均计入);
- 路径上所有时空隧道的通行费用之和。
如果不存在满足条件的路径,则结果为 。
输入格式
第一行包含四个整数 ,分别表示事件节点数、时空隧道数、关键事件的数量和穿越起始节点编号。
第二行包含 个整数 ,表示关键事件集合 中的节点编号。
第三行包含 个整数,第 个整数为事件节点 的伤心值 。
接下来 行,每行包含三个整数 ,表示节点 和 之间存在一条通行费用为 的双向时空隧道。
输出格式
输出共 行,每行一个整数。按目标节点编号升序(排除起始节点 )输出从 到该节点的最小代价,若无法到达则输出 。
样例
5 5 1 3
4
1 2 3 4 5
2 3 4
3 4 5
4 5 6
1 3 2
2 4 1
23
15
12
23
样例解释
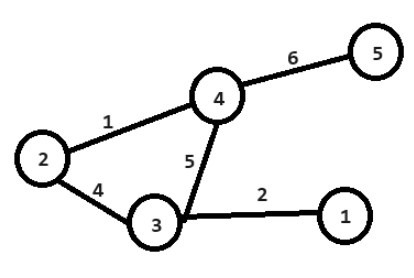
起点 ,关键事件集 。
– 到节点 1 的最优路径需访问节点 4,总代价为 23;
– 其余节点依此类推,分别为 15、12、23。
数据范围
- 对于 的测试数据,保证 $1 \le n \le 10,\;1 \le m \le 50,\;1 \le h_i,w_i \le 100,\;1 \le s \le 5$;
- 对于另 的测试数据,保证 $1 \le n \le 100,\;1 \le m \le 4\times10^3,\;1 \le h_i,w_i \le 100,\;s=1$;
- 对于另 的测试数据,保证 $1 \le n \le 100,\;1 \le m \le 4.5\times10^3,\;1 \le h_i,w_i \le 10^3,\;1 \le s \le 13$;
- 对于另 的测试数据,保证 $1 \le n \le 200,\;1 \le m \le 10^4,\;1 \le h_i,w_i \le 10^3,\;1 \le s \le 5$;
- 对于 的测试数据,保证 $1 \le n \le 500,\;1 \le m \le 6\times10^4,\;1 \le h_i,w_i \le 10^5,\;1 \le s \le 13$,输入无重边、无自环。
后记
当然,时间是无法回到过去的。我们能做的,只有期待未来。
人生漫长,晴雨交加,但若是心怀热爱,即使岁月荒芜,亦能奔山赴海,静待一树花开。
──《人民日报》
